How to Solve Statistics Assignments on Poisson and Binomial Random Variables

In this Probability Theory assignment, we dive into the intriguing world of probability distributions, focusing on two fundamental concepts: Poisson and Binomial Random Variables. Let's explore how these mathematical tools are applied to real-world scenarios and gain a deeper understanding of their significance in statistics and probability theory.

Problem Statement 1: Poisson Random Variable:

In various scenarios, the number of calls received at a call center can be modeled as a Poisson random variable. This is based on the assumption that the rate of incoming calls at the center remains constant throughout the day, and the number of calls received at disjoint intervals of time are independent of each other. If we denote the rate of receiving calls as λ, then within an interval of length t, the number of calls received follows a Poisson distribution, which is represented as follows:

Solution:

The probability mass function for a Poisson random variable with rate parameter λ and within an interval of length t is given by:

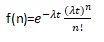
Here, n represents the number of calls received within the specified time interval, λ is the rate of calls, and t is the length of the time interval. This mathematical representation accurately describes the probability distribution of the number of calls, and hence, it is an exemplary instance of a Poisson random variable.

Problem Statement 2: Binomial Random Variable:

Consider a scenario where N individuals have booked tickets for a specific flight. We can assume, based on prior data, that the probability of a person missing the flight is represented by p. Additionally, we can also assume that the individuals who have booked tickets are independent of each other. In this case, the number of persons missing the flight can be modeled as a binomial random variable with parameters N and p, leading to the following distribution:

Solution:

The probability mass function for a binomial random variable with parameters N and p, representing the number of passengers missing the flight, is given by:

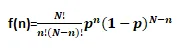
In this formula, N signifies the total number of individuals who booked tickets, n denotes the number of people missing the flight, and p represents the probability of an individual missing the flight. This mathematical representation accurately captures the probability distribution of the number of passengers missing the flight, making it a valid example of a binomial random variable.

Feel free to use these structured explanations for your website as a sample solution for your assignment.