Using Change Point Analysis for Detecting Shifts in Time Series Assignments

Change Point Analysis (CPA) is a powerful statistical technique used to identify points in a time series where the statistical properties of the data change. This method is particularly effective in detecting shifts in mean, variance, or distribution, which may indicate significant changes or events within a system over time. For students working on time series analysis assignments, mastering Change Point Analysis is crucial for obtaining accurate results and drawing meaningful conclusions. It allows them to detect important transitions in data that could otherwise go unnoticed, such as sudden market fluctuations or abrupt changes in environmental factors. By understanding how to implement and interpret Change Point Analysis, students can improve their ability to solve Time Series Assignments with precision. This blog will explore both the theoretical foundations and technical methods behind Change Point Analysis, providing students with the knowledge and practical skills necessary to tackle time series problems confidently and effectively.

What is Change Point Analysis?

Change Point Analysis is a statistical method used to detect abrupt changes in a dataset, particularly in time series data. A time series refers to a sequence of data points collected or recorded at successive time intervals. Detecting change points in this data is essential because it helps identify significant transitions or shifts in the underlying process or system being observed. These changes could manifest as shifts in the mean, variance, or distribution, indicating a change in the behavior of the system. By identifying these change points, analysts can better understand trends, predict future events, and make data-driven decisions.

Key Applications of Change Point Analysis

In real-world applications, Change Point Analysis can be applied across various domains such as finance, healthcare, engineering, and environmental science. Some of the key uses include:

• Financial Markets: Identifying changes in stock price trends or volatility.
• Healthcare: Detecting shifts in patient vitals or disease progression.
• Manufacturing: Spotting changes in machine behavior, indicating potential failures.
• Environmental Monitoring: Recognizing shifts in pollution levels or climate data trends.

Change Point Analysis helps uncover hidden patterns in time series data that might not be immediately obvious, providing better insights for decision-making processes.

Technical Foundation of Change Point Detection

For students learning how to detect change points in time series data, understanding the underlying technical methods is crucial. Let’s break down the fundamental techniques used in Change Point Analysis.

1. The CUSUM (Cumulative Sum) Method

The CUSUM method is one of the most widely used techniques for detecting change points. It involves monitoring the cumulative sum of deviations from a target value (e.g., the mean) over time. When there is a significant deviation from the expected value, it indicates a potential change point.

Steps for Implementing CUSUM:

• Step 1: Calculate the cumulative sum of the deviations from the expected mean.
• Step 2: Define a threshold to indicate when a deviation is significant enough to be considered a change point.
• Step 3: Identify points where the cumulative sum crosses the threshold, signaling a potential shift in the data.

In technical terms, the CUSUM statistic is given by:

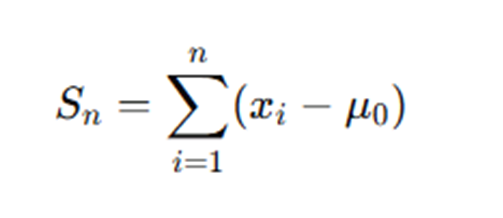
Where:

• Sn is the cumulative sum at time n,
• xi is the observed value at time i,
• μ0 is the reference mean.

2. The PELT (Pruned Exact Linear Time) Algorithm

The PELT algorithm is an efficient method used to detect multiple change points in a time series. Unlike CUSUM, which focuses on detecting a single change point, PELT is designed to handle multiple shifts in the data.

Steps for Implementing PELT:

• Step 1: Fit a cost function (e.g., likelihood or sum of squared errors) to the time series data.
• Step 2: Minimize the cost function by testing different break points and pruning non-optimal candidates.
• Step 3: Identify the change points that result in the best segmentation of the data.

The key advantage of PELT is its computational efficiency, which makes it a popular choice for large datasets with multiple change points.

Understanding Change Point Detection in Practice

Now that we’ve covered the theory and some technical methods for Change Point Analysis, it’s time to explore practical applications in assignments. Here, we’ll cover how to approach assignments that involve detecting shifts in time series data.

Data Preparation and Preprocessing

Before diving into change point detection, it’s essential to prepare and preprocess the data properly. This includes:

• Handling Missing Data: Time series data often contains missing values, which can affect the analysis. Impute or interpolate missing values before proceeding.
• Normalization: Scaling the data can make change point detection algorithms more effective, especially when working with datasets where the range of values varies significantly over time.
• Smoothing: Applying techniques like moving averages can help reduce noise and highlight significant shifts.

1. Implementing CUSUM in Python

For a technical approach, let’s implement the CUSUM method using Python and the numpy library. Here’s an example of how to do this:

Python Code

import numpy as npimport matplotlib.pyplot as plt# Example time series datadata = np.random.normal(loc=50, scale=5, size=100) # Normal distributiondata[60:] += 10 # Introduce a shift in the data# Calculate CUSUMmean = np.mean(data)cusum = np.cumsum(data - mean)# Set threshold for detecting a change pointthreshold = 30change_points = np.where(cusum > threshold)[0]# Plot the data and CUSUMplt.plot(data, label='Time Series Data')plt.plot(cusum, label='CUSUM', color='r')plt.axhline(y=threshold, color='g', linestyle='--', label='Threshold')plt.scatter(change_points, cusum[change_points], color='b', label='Change Points')plt.legend()plt.show()

In this code:

• We generate a time series with a normal distribution and introduce a shift at a certain point.
• We calculate the CUSUM by subtracting the mean from each data point and summing the deviations.
• A threshold is set to identify significant shifts, and potential change points are marked on the plot.

2. Using PELT Algorithm in Python

Here’s an example of implementing the PELT algorithm using the ruptures library in Python:

Python Code

import ruptures as rpt# Example time series datadata = np.random.normal(loc=50, scale=5, size=100)data[60:] += 10 # Introduce a shift in the data# Define the PELT algorithmmodel = "l2" # Model for cost function (sum of squared errors)algo = rpt.Pelt(model=model).fit(data)# Detect change pointschange_points = algo.predict(pen=10)# Plot the resultsrpt.display(data, change_points)plt.show()

In this code:

• The ruptures library is used to implement the PELT algorithm, where the model is set to "l2" for the sum of squared errors.
• The pen parameter controls the penalty for adding additional change points, which helps balance sensitivity to changes with the risk of overfitting.

Challenges and Solutions in Change Point Detection

While Change Point Analysis is a valuable tool, it comes with its own set of challenges. Let’s explore some common issues and how to address them.

1. Handling Noise and Outliers

Noise and outliers in time series data can lead to false positives, where the algorithm detects a change point when there isn’t one. To mitigate this:

• Use smoothing techniques: Moving averages or low-pass filters can help smooth out noise before applying change point detection.
• Robust algorithms: Some change point detection methods, like those based on median absolute deviation (MAD), are more robust to outliers.

2. Choosing the Right Threshold

Choosing the correct threshold for detecting change points is critical. If the threshold is too low, you may detect insignificant changes. If it’s too high, you might miss important shifts.

• Cross-validation: Use cross-validation techniques to find the optimal threshold that balances sensitivity and specificity.
• Automated selection: Some algorithms can automatically adjust the threshold based on the data, reducing the need for manual tuning.

3. Multiple Change Points Detection

In real-world data, there are often multiple change points. Methods like PELT and Binary Segmentation are designed to handle multiple shifts, but they still require careful tuning to avoid overfitting.

• Segmentation validation: After detecting multiple change points, validate each segment to ensure the detected changes are meaningful.

Conclusion:

Change Point Analysis is a crucial technique for detecting shifts in time series data, making it an indispensable tool for students working on time series assignments. By mastering both the theoretical foundations and the technical implementation of methods like CUSUM and PELT, students can gain a deeper understanding of how systems evolve over time and make more accurate conclusions based on their data. To excel in assignments involving Change Point Analysis, students need to not only comprehend the theory but also apply the methods using tools like Python. Preprocessing data, selecting the appropriate algorithms, and fine-tuning parameters are essential steps for students to complete their statistics assignments effectively. By honing these skills, students will be equipped to confidently detect change points and tackle even the most complex time series problems with ease.