How to Solve Statistical Assignments Using Correlation, t-Tests, and ANOVA

Understanding the Assignment Requirements

Before diving into data analysis, carefully read the assignment requirements. Assignments typically involve:

• Evaluating data quality through descriptive analysis.
• Testing statistical assumptions such as normality and homogeneity of variance.
• Performing hypothesis tests like t-tests and ANOVA.
• Comparing results from manual computations and statistical software.

The primary goal is to draw meaningful conclusions from the data while ensuring that all statistical assumptions are met.

Step 1: Data Exploration and Quality Evaluation

Descriptive Statistics

Begin by summarizing the dataset through measures of central tendency (mean, median, mode) and variability (standard deviation, variance, range). This helps in understanding the data distribution before proceeding with formal statistical tests.

Checking Assumptions

• Normality: Use visual methods (histograms, Q-Q plots) and formal tests (Shapiro-Wilk test) to assess if the data follows a normal distribution.
• Influential Outliers: Identify outliers using boxplots and the IQR rule. Extreme values can distort results and should be treated appropriately.
• Variance Homogeneity: Levene’s Test or Bartlett’s Test can confirm if different groups have equal variance, which is essential for ANOVA.

Missing Data Treatment

Missing data can bias results, so handling it properly is crucial. Common methods include:

• Listwise Deletion: Removing cases with missing values.
• Mean/Median Imputation: Replacing missing values with the mean or median.
• Multiple Imputation: Using statistical modeling to estimate missing values.

Step 2: Formulating the Hypotheses

Statistical analysis is grounded in hypothesis testing. Before conducting any test, define:

• Null Hypothesis (H₀): Assumes no difference or no effect (e.g., “There is no difference in academic self-confidence between Classroom 1 and Classroom 2”).
• Alternative Hypothesis (H₁): Suggests a difference exists (e.g., “There is a difference in academic self-confidence between Classroom 1 and Classroom 2”).

Clearly defining these hypotheses helps in selecting the appropriate statistical test and ensures objectivity in analysis.

Step 3: Conducting t-Tests for Group Comparisons

A t-test is used to compare means between two groups.

By-Hand Computation of a Two-Group t-Test

The test statistic is computed as:

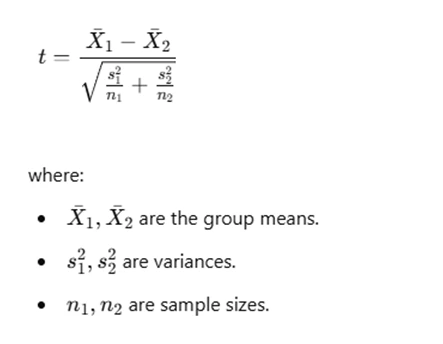
If the calculated t-value exceeds the critical value from the t-distribution table (based on degrees of freedom), we reject the null hypothesis.

Using Statistical Software

• Perform an independent samples t-test.
• Check p-values
• Interpret whether the difference between groups is statistically significant.

Step 4: Conducting One-Way ANOVA for Multiple Group Comparisons

ANOVA is used when comparing more than two groups.

By-Hand Computation of One-Way ANOVA

1. Compute Mean Square Between Groups (MSB):

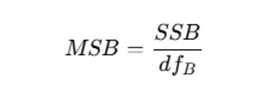
where SSB is the sum of squares between groups and df_B is the degrees of freedom between groups.

2. Compute Mean Square Within Groups (MSW):

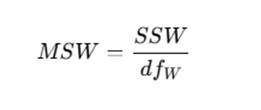
where SSW is the sum of squares within groups and df_W is the degrees of freedom within groups.

3. Compute the F-statistic:

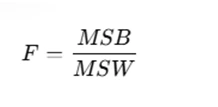
4. Compare the F-value to the critical F-value from statistical tables.

5. If the computed F-value is greater than the critical value, reject the null hypothesis.

Using Statistical Software

• Run a one-way ANOVA.
• Check F-test results and p-values.
• Validate assumptions (normality, homogeneity of variance).
• Compare results with manual calculations.

Step 5: Comparing Results from t-Tests and ANOVA

Both t-tests and ANOVA examine differences between means, but their applications differ:

• t-test is used for two groups.
• ANOVA is used for more than two groups.
• For two groups, t-test and one-way ANOVA should yield the same result.

Effect Size Interpretation

• Cohen’s d: Measures the effect size in t-tests.
• Eta-Squared (n2): Measures the effect size in ANOVA.
• Larger effect sizes indicate stronger relationships between variables.

Step 6: Regression Analysis for Predictive Modeling

Regression analysis allows predicting an outcome variable based on predictor variables.

Simple Linear Regression Equation

Regression results provide insights into how predictor variables influence the outcome and whether the model fits the data well.

Step 7: Interpreting Results and Making Recommendations

• If results show a significant difference, determine practical implications (e.g., should Classroom 1 adopt a different teaching method?).
• If assumptions are violated, consider non-parametric alternatives like the Mann-Whitney U test.
• Report confidence intervals to provide a range of plausible effect sizes.
• Provide actionable recommendations based on statistical findings.

Conclusion

Successfully solving statistical assignments requires a structured approach: exploring data, verifying assumptions, choosing the appropriate test, and interpreting results correctly. Understanding the relationship between different statistical methods, such as t-tests and ANOVA, allows for deeper insights into data and more informed conclusions. Always validate findings using statistical software and theoretical calculations to ensure accuracy and credibility in research outcomes. By mastering these techniques, students can confidently tackle statistical problems and make evidence-based recommendations.