How to Analyze and Solve Regression Assignments with Multicollinearity

Before diving into the specifics of solving regression models with issues such as multicollinearity or autocorrelation, it's important to understand the general framework of a regression model. In the case of the attached assignment, the model attempts to analyze the relationship between a firm's revenue and several key financial metrics, including costs, assets, liabilities, and market value. The goal of such models is to understand how variations in independent variables influence the dependent variable, in this case, revenue.

General Structure of Regression Models

Regression models, especially those in economics and finance, often take the form of linear relationships between a dependent variable and several independent variables. A model may include interactions between variables or transformations, such as logarithmic transformations, to stabilize variance and linearize relationships. The model typically looks like this:

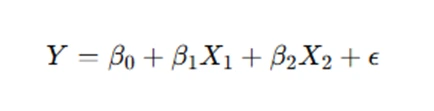
Where:

• Y is the dependent variable.
• X1,X2 are independent variables.
• β0,β1,β2 are coefficients.
• ϵ represents the error term.

The attached assignment uses log transformations of financial variables, which is a common technique to deal with data skewness and heteroscedasticity. This is important because logarithmic transformations help normalize data, making it more suitable for regression analysis.

Identifying and Dealing with Multicollinearity

Multicollinearity is a common issue in regression analysis, particularly when multiple independent variables are highly correlated. It can lead to unstable coefficient estimates, inflated standard errors, and difficulty in interpreting individual predictors. Recognizing multicollinearity early is crucial for accurate model interpretation. Tools like correlation matrices, Variance Inflation Factor (VIF), and condition indices can help identify multicollinearity in your regression model. Once detected, it’s essential to address it through methods such as variable removal, dimensionality reduction techniques like PCA, or using regularization methods like ridge regression. Addressing multicollinearity ensures that your model is both stable and interpretable.

What is Multicollinearity?

In regression analysis, multicollinearity occurs when two or more independent variables in the model are highly correlated with each other. This can cause problems in estimating the relationship between the dependent and independent variables, as it becomes difficult to distinguish the individual effects of correlated variables.

In the attached assignment, variables like cost, assets, and liabilities might be correlated, leading to multicollinearity. Multicollinearity inflates the standard errors of the regression coefficients, making it difficult to assess the true relationship between predictors and the dependent variable.

How to Identify Multicollinearity

There are several methods to identify multicollinearity:

• Correlation Matrix: A correlation matrix can provide an initial understanding of how strongly the independent variables are correlated. If two variables have a high correlation (typically above 0.8 or -0.8), there may be multicollinearity.
• Variance Inflation Factor (VIF): The VIF measures how much the variance of a regression coefficient is inflated due to collinearity with other independent variables. A VIF value greater than 10 is often considered a sign of problematic multicollinearity.
• Condition Index: The condition index is another tool that can be used to detect multicollinearity. A high condition index (greater than 30) suggests that multicollinearity may be present.

How to Address Multicollinearity

If multicollinearity is present, there are several approaches you can take to resolve it:

• Remove Highly Correlated Variables: If two variables are highly correlated, one of them can be removed from the model. For instance, if the cost and liabilities variables are too closely related, removing one may improve model performance.
• Principal Component Analysis (PCA): PCA is a dimensionality reduction technique that can be used to combine correlated variables into a smaller set of uncorrelated components.
• Ridge or Lasso Regression: These techniques add a penalty to the regression, reducing the influence of multicollinearity.

Conducting Statistical Tests and Hypothesis Testing

Statistical tests, like the F-test and t-test, are integral parts of regression analysis. These tests help determine the significance of the overall model (F-test) and individual coefficients (t-test). The F-test evaluates whether the independent variables collectively explain a significant portion of the variation in the dependent variable, while the t-test assesses whether a specific predictor has a meaningful effect. Both tests provide valuable insights into model fit and variable importance. Conducting these tests ensures that your model is reliable and that you’re drawing valid conclusions about the relationships between variables, guiding your interpretation of results.

F-Tests and t-Tests in Regression

Regression models often require hypothesis testing to determine whether the relationships between variables are statistically significant. For example, in the attached assignment, part of the task involves conducting an F-test and t-tests.

F-Test

The F-test evaluates whether at least one of the independent variables in the model has a non-zero coefficient. This is important because it tells you if your model as a whole is statistically significant.

For instance, if the regression model includes multiple predictors, the F-test examines if the joint effect of all predictors is statistically significant.

t-Test

The t-test is used to test the significance of individual regression coefficients. It determines if a particular predictor variable has a significant relationship with the dependent variable.

For example, if testing the effect of the debt ratio on revenue, you would use the t-test to assess whether the coefficient for the debt ratio is significantly different from zero.

Model Specification and Improvements

Model specification is the process of defining a regression model with the right set of variables and functional form. A well-specified model accurately captures the relationships between the dependent and independent variables. If multicollinearity or other issues are present, it’s necessary to revise the model to enhance its reliability. This can involve removing problematic variables, adding interaction terms to capture joint effects, or applying transformations like logarithms to stabilize variance. Model improvements also involve ensuring that assumptions such as linearity and homoscedasticity are met, which strengthens the validity of the regression results and their interpretability.

Revising the Model to Address Issues

When issues such as multicollinearity are detected, you may need to revise the regression model. This may involve:

• Dropping Collinear Variables: If two variables are highly correlated, dropping one of them may improve the model's stability and reduce multicollinearity.
• Adding Interaction Terms: If interactions between variables are suspected (for example, costs and assets), adding interaction terms can improve the model's fit.
• Log Transformation Adjustments: The log transformations in the model may need to be adjusted based on the correlation structure of the data.

By re-specifying the model, you can ensure that the regression results are valid and meaningful.

Addressing Other Common Statistical Problems

In regression analysis, it’s important to recognize and address other statistical issues like autocorrelation and the use of dummy variables. Autocorrelation, where residuals are correlated with one another, can distort coefficient estimates and undermine the model’s reliability. The Durbin-Watson test is commonly used to detect autocorrelation and help adjust the model accordingly. Additionally, when dealing with categorical variables, dummy variables are used to represent them in regression models. Proper interpretation of dummy variable coefficients and addressing autocorrelation ensures that the regression analysis is robust and the results are meaningful, leading to more accurate conclusions.

Autocorrelation and Its Impact

Autocorrelation occurs when the residuals (errors) in a regression model are correlated with each other. This violates the assumption that errors are independently distributed, which can lead to biased coefficient estimates.

Durbin-Watson Test

The Durbin-Watson test is commonly used to detect autocorrelation. A test statistic close to 2 suggests no autocorrelation, while values significantly less than or greater than 2 indicate positive or negative autocorrelation, respectively.

The Role of Dummy Variables

In some regression models, like the one in the attached assignment, dummy variables (e.g., union membership, college graduation) are used to represent categorical data. Dummy variables are useful for modeling binary outcomes, and their coefficients are interpreted as the difference in the dependent variable for each category relative to the baseline group.

Conclusion

Solving assignments involving regression models, especially those addressing multicollinearity, autocorrelation, and model specification, requires a comprehensive understanding of both statistical theory and practical problem-solving skills. In assignments like the one provided, the task goes beyond merely running regression models; it involves diagnosing potential issues such as multicollinearity and autocorrelation that can distort the results. These problems, if not addressed, can lead to unreliable conclusions. By following a structured approach to analysis, including performing tests like the Variance Inflation Factor (VIF) and the Durbin-Watson test, students can successfully identify and rectify these issues. A methodical approach to model specification and improvement ensures more accurate and meaningful results. When you need to complete your statistics assignments, whether dealing with regression models or other challenges, mastering these techniques will not only help you solve complex problems but will also be invaluable for achieving success in your academic journey. These skills will set you apart and lead to better understanding and application of statistical concepts.