The Role of Simulated Annealing in Optimizing Statistics Assignments
Avail Your Offer
Unlock success this fall with our exclusive offer! Get 20% off on all statistics assignments for the fall semester at www.statisticsassignmenthelp.com. Don't miss out on expert guidance at a discounted rate. Enhance your grades and confidence. Hurry, this limited-time offer won't last long!
We Accept
- Understanding Simulated Annealing: A Statistical Perspective
- Applications of Simulated Annealing in Statistics Assignments
- Parameter Estimation in Regression Models
- Linear Regression with Simulated Annealing
- Logistic Regression Optimization
- Solving Combinatorial Problems in Statistics
- Clustering with Simulated Annealing
- Network Optimization
- High-Dimensional Statistical Analysis
- Principal Component Analysis (PCA)
- Feature Selection
- Time-Series Analysis and Forecasting
- Parameter Optimization in ARIMA Models
- Anomaly Detection in Time-Series
- Best Practices for Using Simulated Annealing in Assignments
- Practical Tips for Implementing SA
- Choosing a Cooling Schedule
- Defining the Cost Function
- Conclusion
Simulated Annealing (SA) is a robust and versatile optimization algorithm, drawing inspiration from the physical process of annealing in metallurgy, where metals are heated and gradually cooled to increase their strength and reduce defects. This analogy is at the heart of SA, where the algorithm explores a solution space by imitating this controlled cooling process. It has become an indispensable tool for solving intricate statistical problems, especially in domains that involve high-dimensional data, complex combinatorial optimization, and parameter estimation. Unlike traditional optimization techniques, which often get trapped in local minima, simulated annealing is designed to escape these pitfalls by probabilistically accepting worse solutions during its search, enabling a more comprehensive exploration of the solution space. For students seeking help with statistics assignments, SA offers a powerful method to tackle complex optimization challenges. This blog delves into the practical applications of simulated annealing in statistics assignments, blending theoretical insights with technical examples to empower students with the tools and understanding needed to address their most challenging academic problems effectively.
Understanding Simulated Annealing: A Statistical Perspective
Simulated Annealing (SA) is a computational method inspired by the thermodynamic process of cooling materials to achieve a stable structure. In statistics, it is a powerful tool for optimization, enabling solutions to complex problems with minimal assumptions about the data. By balancing exploration and exploitation, SA offers a flexible approach to navigate multidimensional spaces, making it an essential technique for tackling statistical challenges effectively.
What Is Simulated Annealing?
Simulated Annealing is a probabilistic optimization technique that mimics the cooling process of metals. It iteratively searches for a global minimum of a cost function, allowing temporary acceptance of worse solutions to escape local minima.
Key Components:
- Cost Function: Represents the problem to be optimized (e.g., minimizing error in regression).
- Temperature: A control parameter that reduces over iterations, influencing the acceptance probability of suboptimal solutions.
- Cooling Schedule: Determines how the temperature decreases.
Why Use Simulated Annealing in Statistics?
Statistical problems often involve multidimensional search spaces, where traditional optimization methods may fail due to local minima or computational infeasibility. Simulated annealing:
- Handles complex, nonlinear cost functions.
- Requires fewer assumptions about the problem structure.
- Is robust against noisy or incomplete data.
Applications of Simulated Annealing in Statistics Assignments
Simulated Annealing has proven to be a game-changer in various statistical domains due to its adaptability and effectiveness in finding optimal or near-optimal solutions. In the context of statistics assignments, this algorithm is particularly valuable for tackling problems that are computationally intensive or involve non-linear and high-dimensional data. By mimicking the natural process of annealing, SA systematically explores the solution space, balancing exploration and exploitation to identify solutions that might otherwise be overlooked by conventional optimization methods.
This section highlights how simulated annealing can be applied to common challenges in statistics, including parameter estimation, clustering, and high-dimensional analysis. Through technical examples and step-by-step implementation strategies, students can gain a practical understanding of using SA to overcome these challenges, improving both the accuracy and efficiency of their solutions. Whether dealing with regression models, combinatorial optimization, or time-series forecasting, SA offers a reliable approach to achieving robust results.
Parameter Estimation in Regression Models
Parameter estimation is a critical task in regression analysis, where the goal is to determine the best-fitting parameters (such as coefficients) for a given model. Traditional methods like Ordinary Least Squares (OLS) are widely used, but they can struggle with issues like multicollinearity, non-linearity, or the presence of outliers. In such cases, Simulated Annealing (SA) offers a valuable alternative by providing a flexible and robust way to optimize the parameters of the regression model.
Using SA, students can tackle complex regression problems where other methods might fail or be computationally expensive. The algorithm allows for the exploration of the solution space to find the optimal parameters that minimize the error function, even in high-dimensional settings or when the dataset contains noisy or missing values. In this section, we will explore how SA can be used for parameter estimation in linear and nonlinear regression models, demonstrating its practical application in solving real-world statistics assignments.
Linear Regression with Simulated Annealing
Parameter estimation in regression involves minimizing the error function, such as the Mean Squared Error (MSE). Simulated annealing can optimize coefficients effectively, even in cases with multicollinearity or missing data.
Example: Consider the linear regression model:
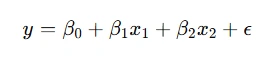
Here’s a Python implementation using SA for optimizing β0,β1,β2:
import numpy as np
import random
# Simulated Annealing for Linear Regression
def cost_function(params, x, y):
predictions = params[0] + params[1] * x[:, 0] + params[2] * x[:, 1]
return np.mean((y - predictions) ** 2)
def simulated_annealing(x, y, initial_params, temp, cooling_rate, iterations):
current_params = np.array(initial_params)
current_cost = cost_function(current_params, x, y)
best_params = current_params.copy()
best_cost = current_cost
for i in range(iterations):
new_params = current_params + np.random.normal(0, temp, size=current_params.shape)
new_cost = cost_function(new_params, x, y)
if new_cost < current_cost or np.exp((current_cost - new_cost) / temp) > random.random():
current_params = new_params
current_cost = new_cost
if current_cost < best_cost:
best_params = current_params
best_cost = current_cost
temp *= cooling_rate
return best_params, best_cost
# Example dataset
x_data = np.random.rand(100, 2)
y_data = 3 + 2 * x_data[:, 0] - 4 * x_data[:, 1] + np.random.normal(0, 0.5, 100)
# Optimize parameters
params, cost = simulated_annealing(x_data, y_data, [0, 0, 0], 10, 0.95, 1000)
print("Optimized Parameters:", params)
print("Final Cost:", cost)
Logistic Regression Optimization
In classification problems, SA can optimize the log-likelihood function for logistic regression, improving model accuracy in datasets with imbalanced classes.
Solving Combinatorial Problems in Statistics
Combinatorial problems in statistics often involve finding optimal solutions to challenges that have a large number of possible configurations, such as clustering, feature selection, or optimization in network models. These problems can be computationally difficult due to the sheer size of the solution space, making traditional methods inefficient or infeasible. This is where Simulated Annealing (SA) becomes an invaluable tool.
By applying SA, students can efficiently explore combinatorial spaces to find optimal or near-optimal solutions. The algorithm’s probabilistic nature allows it to escape local optima, providing a better chance of finding a global optimum even in complex combinatorial scenarios. Whether it’s optimizing clustering assignments in high-dimensional datasets or selecting a minimal set of features for a regression model, SA helps in overcoming the limitations of more conventional methods. In this section, we will explore the role of SA in tackling combinatorial problems in statistics, providing technical insights and examples that can guide students through solving such challenging assignments.
Clustering with Simulated Annealing
Simulated annealing can enhance clustering algorithms like K-Means by optimizing cluster assignments. Instead of starting with random centroids, SA explores multiple configurations to minimize intra-cluster variance.
Technical Example: Using SA to optimize K-means clustering.
from sklearn.datasets import make_blobs
from sklearn.metrics import pairwise_distances_argmin
# Dataset for clustering
X, _ = make_blobs(n_samples=100, centers=3, cluster_std=0.60, random_state=42)
# Cost function: Sum of squared distances to cluster centers
def clustering_cost(centroids, data, labels):
return sum(np.linalg.norm(data[i] - centroids[labels[i]])**2 for i in range(len(data)))
# SA for clustering
def sa_clustering(data, k, temp, cooling_rate, iterations):
centroids = data[np.random.choice(len(data), k, replace=False)]
labels = pairwise_distances_argmin(data, centroids)
current_cost = clustering_cost(centroids, data, labels)
best_centroids = centroids.copy()
best_cost = current_cost
for _ in range(iterations):
new_centroids = centroids + np.random.normal(0, temp, centroids.shape)
new_labels = pairwise_distances_argmin(data, new_centroids)
new_cost = clustering_cost(new_centroids, data, new_labels)
if new_cost < current_cost or np.exp((current_cost - new_cost) / temp) > random.random():
centroids, labels = new_centroids, new_labels
current_cost = new_cost
if current_cost < best_cost:
best_centroids = centroids
best_cost = current_cost
temp *= cooling_rate
return best_centroids, best_cost
final_centroids, final_cost = sa_clustering(X, 3, 10, 0.95, 100)
print("Final Centroids:", final_centroids)
Network Optimization
SA helps in network flow optimization problems by minimizing the cost of statistical operations, such as minimizing path costs or optimizing data communication in Bayesian networks.
High-Dimensional Statistical Analysis
High-dimensional statistical analysis deals with datasets that have a large number of variables or features, often leading to challenges such as overfitting, computational complexity, and the curse of dimensionality. In these situations, traditional statistical methods may struggle to provide accurate or efficient solutions due to the sheer volume of data and the complexity of interactions between variables. Simulated Annealing (SA) offers an effective approach to tackling these high-dimensional problems by optimizing functions in spaces with many dimensions.
SA's ability to explore large, complex search spaces makes it particularly useful for dimensionality reduction techniques, like Principal Component Analysis (PCA), and for feature selection in regression or classification tasks. It also helps in overcoming issues such as noise and multicollinearity that are common in high-dimensional datasets. In this section, we will explore how SA can be applied to high-dimensional statistical problems, illustrating its power in optimizing models, reducing dimensions, and improving the accuracy and interpretability of statistical results in real-world assignments.
Principal Component Analysis (PCA)
When traditional PCA struggles with non-convex optimization, SA can help find the optimal projection that maximizes variance.
Feature Selection
SA effectively selects the most relevant features for regression or classification, optimizing model performance and reducing computation time.
Time-Series Analysis and Forecasting
Time-series analysis and forecasting are essential tools in statistics, used to analyze temporal data and predict future values based on historical trends. These problems often involve intricate patterns, seasonality, and noise, making them challenging for traditional statistical methods. Simulated Annealing (SA) provides a flexible and robust optimization technique for solving complex time-series problems, particularly in scenarios where conventional methods may not be effective or scalable.
By applying SA, students can optimize model parameters for time-series forecasting methods, such as autoregressive integrated moving average (ARIMA) models or machine learning-based approaches. The algorithm can be used to fine-tune parameters like lag values, smoothing coefficients, or feature selection in a way that enhances the model's predictive accuracy. Furthermore, SA’s ability to escape local minima and explore broader solution spaces makes it particularly suitable for identifying hidden patterns in noisy or volatile time-series data. In this section, we will explore the role of SA in time-series analysis and forecasting, with examples demonstrating how it can be applied to real-world statistical assignments involving temporal data.
Parameter Optimization in ARIMA Models
Simulated Annealing fine-tunes ARIMA model parameters (p, d, q) for time-series forecasting, minimizing prediction errors.
Anomaly Detection in Time-Series
By optimizing thresholds for anomaly detection algorithms, SA enhances accuracy in identifying unusual patterns in statistical data.
Best Practices for Using Simulated Annealing in Assignments
While Simulated Annealing (SA) is a powerful optimization tool, its effectiveness depends on how well it is implemented and tuned for the specific problem at hand. In statistics assignments, applying SA requires a careful understanding of the algorithm’s parameters, the nature of the problem, and the dataset characteristics. By following best practices, students can ensure they make the most of this technique and achieve optimal or near-optimal results efficiently.
This section will provide key guidelines for using SA in statistics assignments, focusing on how to properly configure the algorithm, handle large or noisy datasets, and interpret results. Topics will include setting appropriate temperature schedules, selecting the right neighborhood function, ensuring convergence, and avoiding common pitfalls such as premature convergence or poor exploration of the solution space. By following these best practices, students can optimize their problem-solving approach and significantly enhance the quality of their assignments.
Practical Tips for Implementing SA
Implementing Simulated Annealing (SA) in your statistics assignments requires a balance between understanding the underlying theory and applying it effectively in practice. While the algorithm’s concept is relatively simple, its implementation can be complex due to the need for fine-tuning various parameters and adapting it to specific problems. In this section, we will provide practical tips to help you get the most out of SA in your assignments.
These tips will cover crucial aspects such as selecting the initial solution, designing an effective cooling schedule, and deciding on the appropriate move function for your problem. We’ll also discuss how to implement SA in common statistical tasks like parameter optimization and feature selection, providing students with hands-on techniques to apply in real-world scenarios. By following these practical tips, students can efficiently use SA to solve optimization problems in statistics, improve their assignments, and gain a deeper understanding of advanced optimization techniques.
Choosing a Cooling Schedule
A slower cooling schedule (e.g., exponential decay) provides better convergence but requires more iterations.
Defining the Cost Function
Tailor the cost function to align closely with the statistical objective, such as minimizing MSE or maximizing likelihood.
Conclusion
Simulated Annealing is a versatile tool for optimizing complex statistical problems. Whether it's parameter estimation, clustering, or high-dimensional data analysis, SA offers robust solutions that traditional methods may not. By combining theoretical understanding with hands-on implementation, students can effectively tackle their statistics assignments and develop a deeper appreciation for optimization techniques.