Using PROC PHREG for Advanced Survival Analysis in SAS Assignments
Avail Your Offer Now
Celebrate the festive season with an exclusive holiday treat! Enjoy 15% off on all orders at www.statisticsassignmenthelp.com this Christmas and New Year. Unlock expert guidance to boost your academic success at a discounted price. Use the code SAHHOLIDAY15 to claim your offer and start the New Year on the right note. Don’t wait—this special offer is available for a limited time only!
We Accept
- Understanding Survival Analysis and Cox Proportional Hazards Model
- What is Survival Analysis?
- The Role of the Cox Proportional Hazards Model
- Key Features of PROC PHREG in SAS
- Preparing Data for PROC PHREG Analysis
- Formatting Time-to-Event Data
- Creating Categorical Variables and Dummy Coding
- Running a Basic Cox Proportional Hazards Model with PROC PHREG
- Syntax of PROC PHREG
- Output Interpretation
- Advanced Techniques in PROC PHREG for Survival Analysis
- Time-Varying Covariates in Cox Regression
- Stratification in Cox Models
- Validating the Assumptions of the Cox Model
- Checking Proportional Hazards Assumption
- Diagnostics and Model Checking
- Conclusion
Survival analysis is a vital statistical technique used to analyze and interpret the time until an event of interest occurs. This type of analysis is essential in various fields such as medicine, engineering, and social sciences, where understanding time-to-event data is crucial. In SAS, PROC PHREG stands out as one of the primary procedures for conducting advanced survival analysis, particularly when dealing with Cox proportional hazards models. These models help analyze how different variables affect the likelihood of an event occurring over time. For students working with survival analysis in SAS, PROC PHREG provides a powerful tool for solving complex survival-related questions. In this blog post, we'll delve into the use of PROC PHREG, offering students a comprehensive guide on how to effectively apply this procedure to solve their SAS assignments. Whether you're analyzing healthcare data, financial data, or engineering experiments, mastering PROC PHREG can help you achieve accurate results and excel in your assignments.
Understanding Survival Analysis and Cox Proportional Hazards Model
In any survival analysis project, the first step is understanding the fundamentals of the method and the model you will apply. The Cox proportional hazards model is central to survival analysis, helping you interpret how covariates influence the time until an event happens. PROC PHREG is specifically designed to help you implement this model efficiently and extract meaningful insights from your data.
What is Survival Analysis?
Survival analysis focuses on the analysis of time-to-event data, which typically involves estimating the time until the event of interest occurs, such as death, failure, or recovery. The data are usually censored, meaning that the event has not yet occurred for some individuals by the end of the study. This makes survival analysis particularly useful in fields like medical research, where some patients may drop out of a study before experiencing the event.
In SAS, survival analysis is typically performed using procedures like PROC LIFETEST for non-parametric methods and PROC PHREG for regression models such as the Cox proportional hazards model. The Cox model is used to assess the relationship between the survival time of individuals and one or more predictor variables.
The Role of the Cox Proportional Hazards Model
The Cox proportional hazards model is a semiparametric regression model that allows the estimation of the hazard ratio, which is the ratio of the hazard for an individual with a certain set of covariates relative to another individual with a different set of covariates. The Cox model assumes that the hazard at any time point is a function of a baseline hazard and the effects of explanatory variables.
The general form of the Cox proportional hazards model is:
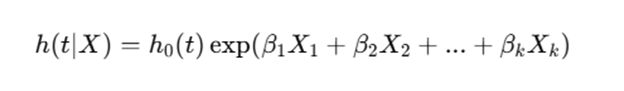
Where:
- h(t|X) is the hazard function at time t for a person with covariates X,
- h0(t) is the baseline hazard at time t,
- β1,β2,...,βk are the regression coefficients,
- X1,X2,...,Xk are the covariates.
Key Features of PROC PHREG in SAS
PROC PHREG is designed to perform Cox regression analysis in SAS. It can be used for a variety of purposes, including:
- Fitting Cox models with continuous or categorical covariates.
- Testing hypotheses about the effect of covariates on the hazard.
- Estimating survival probabilities for different groups based on the model.
- Handling time-varying covariates.
By using PROC PHREG, students can estimate the impact of various predictors on survival outcomes, interpret hazard ratios, and predict survival probabilities based on their data.
Preparing Data for PROC PHREG Analysis
Before diving into the analysis using PROC PHREG, it's essential to ensure that your data is formatted correctly. Proper data preparation is crucial to ensure the accuracy and reliability of your survival analysis results.
Formatting Time-to-Event Data
To use PROC PHREG, the dataset needs to contain two key variables: one for the time-to-event and one for the status indicator. The time-to-event variable represents the duration until the event of interest occurs, while the status indicator (usually a binary variable) indicates whether the event was observed (1) or censored (0).
Here’s an example of how a dataset might look:
| PatientID | Time | Status | Age | Treatment |
|---|---|---|---|---|
| 1 | 5 | 1 | 60 | A |
| 2 | 8 | 0 | 55 | B |
| 3 | 3 | 1 | 70 | A |
| 4 | 7 | 1 | 65 | B |
In this dataset:
- Time represents the survival time (in months, for example),
- Status indicates whether the patient experienced the event (1 for event, 0 for censored),
- Age is a continuous covariate,
- Treatment is a categorical covariate indicating the treatment type (A or B).
Creating Categorical Variables and Dummy Coding
If your dataset contains categorical variables, you may need to create dummy variables to include them in the model. For example, if Treatment is a categorical variable with two levels (A and B), SAS will automatically create a reference group (A in this case) and estimate the effect of the other category (B) in relation to this reference.
data survival_data;
set raw_data;
if Treatment = 'A' then Treatment_A = 1;
else Treatment_A = 0;
run;
Now, you can use this dummy-coded variable in the PROC PHREG model.
Running a Basic Cox Proportional Hazards Model with PROC PHREG
Once your data is properly prepared, you can start fitting a basic Cox proportional hazards model using PROC PHREG. This is where you will apply your statistical knowledge to run the model and interpret the results.
Syntax of PROC PHREG
The syntax for PROC PHREG is relatively simple. Let’s run a basic Cox regression model to analyze the effect of Age and Treatment on survival time. The basic syntax is as follows:
proc phreg data=survival_data;
class Treatment;
model Time*Status(0) = Age Treatment;
run;
Explanation:
- data=survival_data: Specifies the input dataset.
- class Treatment: Specifies that Treatment is a categorical variable.
- model Time*Status(0) = Age Treatment: Specifies the survival model. Here, Time is the time-to-event variable, Status is the censoring indicator (with 0 for censored), and Age and Treatment are the predictors.
- The model will estimate the effect of Age and Treatment on the hazard of the event occurring.
Output Interpretation
The output will include the following key information:
- Hazard Ratios (HR): These values represent the ratio of the hazard for one unit increase in the predictor variable, adjusted for the other variables in the model.
- Confidence Intervals (CI): These intervals give the range within which the true hazard ratio lies with a certain level of confidence (typically 95%).
- P-values: These values help in testing the null hypothesis that the corresponding coefficient is equal to zero (no effect). A p-value less than 0.05 typically indicates statistical significance.
Advanced Techniques in PROC PHREG for Survival Analysis
As you progress in your analysis, you may encounter more complex datasets or situations that require advanced modeling techniques. SAS offers several powerful tools within PROC PHREG for handling such cases.
Time-Varying Covariates in Cox Regression
One of the advanced features of PROC PHREG is its ability to handle time-varying covariates. Time-varying covariates change over time and must be treated differently in the model. For example, a patient’s treatment type may change during the study, or the patient may experience a new risk factor that could affect survival.
Here’s an example of using a time-varying covariate:
proc phreg data=survival_data;
class Treatment;
model Time*Status(0) = Age Treatment / ties=exact;
test Age, Treatment;
run;
In this case, the test statement tests the significance of Age and Treatment. If Age and Treatment are interacting over time, the test will help determine the significance of this interaction.
Stratification in Cox Models
In some cases, you may want to account for differences in the baseline hazard for different strata (groups). For example, stratification might be used when the proportional hazards assumption is violated.
Here’s how to implement stratification in PROC PHREG:
proc phreg data=survival_data;
class Treatment;
model Time*Status(0) = Age / strata=Gender;
run;
In this example, Gender is used as a stratification variable. The model will estimate separate baseline hazards for males and females, while still estimating the effect of Age on survival.
Validating the Assumptions of the Cox Model
A critical part of survival analysis is ensuring that the assumptions underlying the model are met. PROC PHREG provides several tools to test and validate these assumptions.
Checking Proportional Hazards Assumption
A key assumption in the Cox model is that the hazards are proportional over time. You can check this assumption using graphical methods, such as plotting the scaled Schoenfeld residuals, or through formal tests in PROC PHREG.
Here’s how to test the proportional hazards assumption:
proc phreg data=survival_data;
model Time*Status(0) = Age Treatment;
assess ph / resample;
run;
If the proportional hazards assumption holds, the residuals should show no pattern over time. If there is a trend, it suggests that the hazards may not be proportional, and alternative modeling techniques might be needed.
Diagnostics and Model Checking
You can also use diagnostics to check the adequacy of the model, for example, by examining residuals or influence statistics. PROC PHREG provides options for examining residuals, which can help identify outliers or influential data points.
proc phreg data=survival_data;
model Time*Status(0) = Age Treatment;
output out=diagnostics r=residuals;
run;
This will create a dataset diagnostics that includes the residuals, which can then be examined to identify any unusual patterns or influential observations.
Conclusion
PROC PHREG is a powerful tool in SAS for performing advanced survival analysis, especially for fitting Cox proportional hazards models. By understanding the syntax and applying it to real-world data, students can gain valuable insights into survival analysis. In this blog post, we covered the basic steps of using PROC PHREG, advanced techniques such as handling time-varying covariates, and checking the validity of model assumptions.
For students working on assignments involving survival analysis, this guide provides a practical framework for applying PROC PHREG to real datasets. By mastering this procedure, you’ll be well-equipped to tackle more complex survival analysis problems in SAS and excel in your statistics assignments.